Thinking in Chain: How to build GFQL queries

GFQL querying is entirely built around the "chain" function. All possible queries in GFQL can be expressed in terms of a series of chain GFQL operations. This includes any queries which can be performed using the "hop" function (a specialized implementation of chain optimized for specific operations).

Chain operations tell the algorithm how a subgraph should be extracted from any given graph. Much like in Cypher query language, another graph query language, chain queries are declarative; meaning that instead of writing code instructions on how to extract a subgraph from the graph, instead a user can simply describe the subgraph that they want to extract in terms of node properties, edge properties, and relationships.

This document will explain, in approachable terms, the behind-the-scenes of the GFQL algorithm and in the process provide an intuitive understanding of how to use GFQL queries to extract subgraphs from your network graph, and if desired tag elements in your subgraph.

An analogy

A good way to understand how chain works is to use a map analogy. First, lets build a small network graph representative of a small geographical area. Imagine that we have a series of locations connected by roads and each of these locations are represented by nodes. Every node belongs to a town and there is one point of interest at each location, which can be "Grocery store", a "Movie theatre", a "Pet shop", etc. Edges represent direct road connections between locations and are nondirectional (say there are no one way roads in this area).

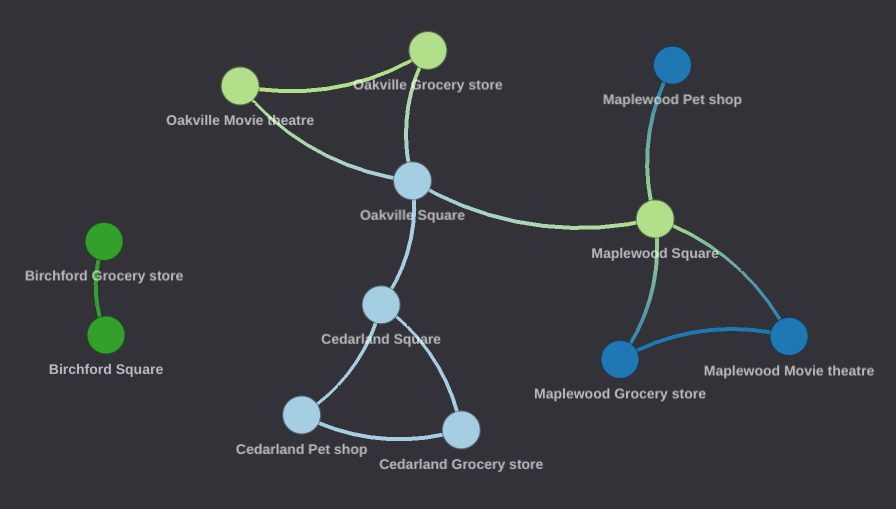
Now imagine that we are interested in finding all the grocery stores in the area that have a direct road connection to a movie theatre.

So what we can do is send out our friends to every single location in the area and ask them, "is this a grocery store"? We can instruct them that if the location is a grocery store, then await further instructions. If the location is not a grocery store, then they can go home; their job is done. In terms of our series of GFQL operations, our first operation looks like the following: look for all elements of type "Node" that contains a property key "point_of_interest" with the property value "grocery store".

{
    "type": "Node",
    "filter_dict": {
        "point_of_interest": "Grocery store"
    }
}

Our next step is to ask our friends standing at a grocery store to send someone down all roads directly connected to your grocery store. In terms of our series of GFQL operations, our second operation looks like the following: from the potential subgraph elements found at this point, disregarding edge direction, look for one element of type "Edge" (that is one hop out) connected to the existing subgraph. The "to_fixed_point" property indicates that this token should not be matched greedily and use the hops value specified; this property will be explained with greater clarity further on.

{
    "type": "Edge",
    "direction": "undirected",
    "hops": 1,
    "to_fixed_point": False
}

Our last step is to ask our friends that went down each road in the previous step, send someone to look at the location at the end of that road, if it is a movie theatre, then await further instructions. If the location is not a movie theatre, they can go home. In terms of our series of GFQL operations, our third operation looks like the following: from the potential subgraph elements found at this point, look for all elements of type "Node" that contains a property key "point_of_interest" with the property value "movie theatre".

{
    "type": "Node",
    "filter_dict": {
        "point_of_interest": "Movie theatre"
    }
}

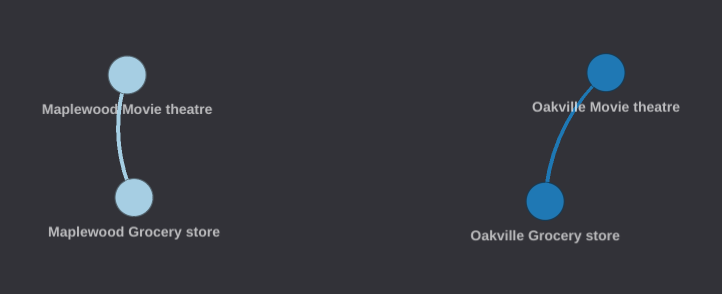
The last thing to do is ask everyone to report back to us what they found. All of our friends at a movie theatre know the path that they (or the buddies that sent them) took to get there from the grocery store that they started out at. They will now inform us of all the roads and locations they have visited on their trip. We take all of their roads and locations and we are done! We now have a list of all the grocery store locations in the area that have a direct road connection to the movie theatre and all movie theatre locations that have a direct road connection to a grocery store, and we have a list of all the roads linking any grocery store to a movie theatre and vice versa.

To bring this back to graph terms, we now have a list of all nodes and edges traversed that match the pattern we have defined, that pattern being the list of GFQL operations that we used to get to this point. In summary, this query can be written as follows:

[
    {
        "type": "Node",
        "filter_dict": {
            "point_of_interest": "Grocery store"
        }
    },
    {
        "type": "Edge",
        "direction": "undirected",
        "hops": 1,
        "to_fixed_point": False
    },
    {
        "type": "Node",
        "filter_dict": {
            "point_of_interest": "Movie theatre"
        }
    }
]

If the query is run on the network graph representing the geographical area shown earlier, the following result is returned.

Getting greedy, leaving breadcrumbs

Another question we can ask about the map is, for every road in the area, which ones are connected at all to "Oakville Square"? Similar to before, we can start with a simple node filter. We know that although all locations will be checked, from our prior knowledge of the map only one location will be returned, "Oakville Square".

{
    "type": "Node",
    "filter_dict": {
        "town": "Oakville",
        "point_of_interest": "Square"
    }
}

Now lets do something completely new. Next, tell our friend at "Oakville Square", send people down any road connected to "Oakville Square", and mark that road "connected_to_Oakville_Square". If they find any new roads at the end of that road that one of our people have not visited yet, send someone down that road and tell them to follow the exact same instructions that you were given (go down the road, send someone down any new roads found, and mark the road with "connected_to_Oakville_Square"). At the risk of bringing in yet another analogy, this is the same thing that "greedy quantifiers" used in regular expressions do.

In terms of our series of GFQL operations, our second operation looks like the following: from the potential subgraph elements found at this point, disregarding edge direction, look for an element of type "Edge" connected to the existing subgraph and tag the edge with "connected_to_Oakville_Square". For any new edge elements found at the end of that edge, keep repeating the above instructions until all possible matching elements are exhausted.

{
    "name": "connected_to_Oakville_Square",
    "type": "Edge",
    "direction": "undirected",
    "to_fixed_point": True
}

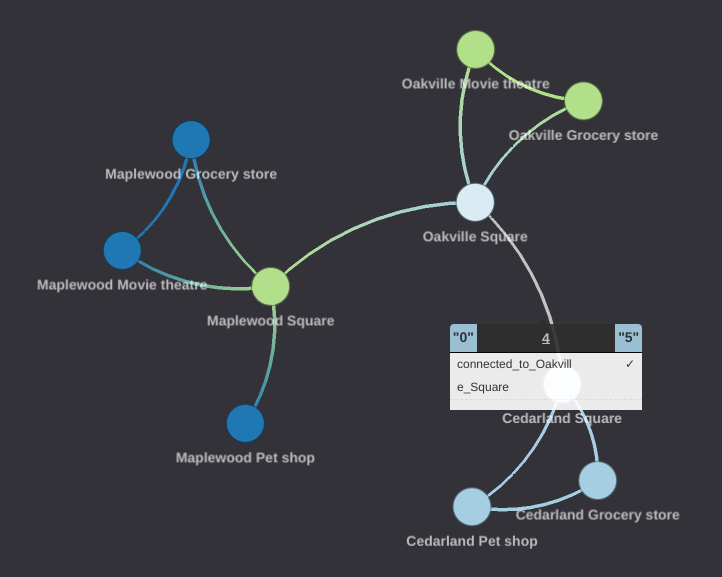
When everything is done, once again we can ask all our friends that have reached the metaphorical "end of the road" to report back to us on the roads they have traversed and any marks that they have made and we are done! We now have a list of all roads and locations that are connected to "Oakville Square", and every road has a tag attached that indicates if it is connected to "Oakville Square"

As before, to bring this back to graph terms, we now have a list of all nodes and edges traversed that match the pattern we have defined, that pattern being the list of GFQL operations that we used to get to this point. In summary, this query can be written as follows:

[
    {
        "type": "Node",
        "filter_dict": {
            "town": "Oakville",
            "point_of_interest": "Square"
        }
    },
    {
        "name": "connected_to_Oakville_Square",
        "type": "Edge",
        "direction": "undirected",
        "to_fixed_point": True
    }
]

If the query is run on the network graph representing the geographical area shown earlier, the following result is returned.

Final remarks

The following example, through the lens of a friendly analogy, should hopefully allow you to develop an intuition on how to use a list of GFQL operations to query a network graph loaded into graphistry. Click here for more information on how to use GFQL using an endpoint. Click here for more information about the options which can be used in the construction of GFQL operations.